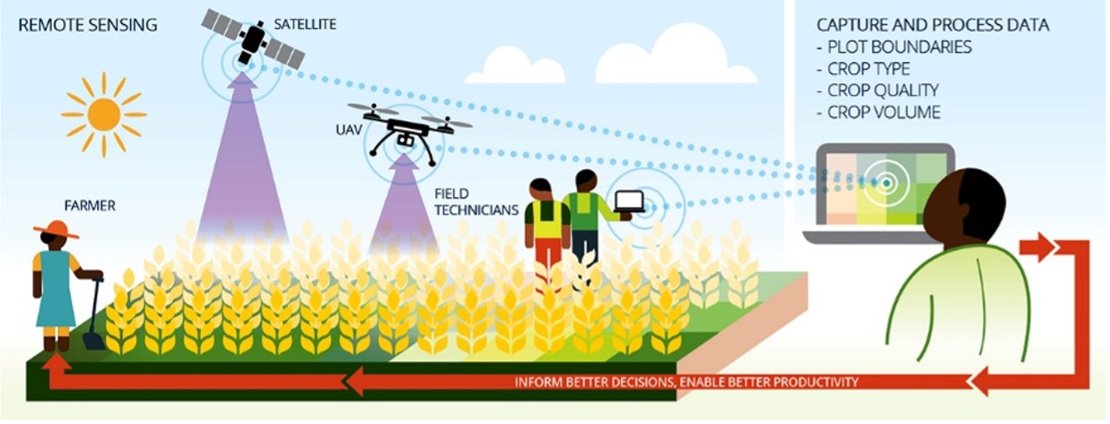
STARS was a project looking for ways to use high resolution remote sensing technology to improve small-scale agriculture in Sub-Saharan Africa and South Asia. Supported by the Bill & Melinda Gates Foundation, the project aimed to develop information products that help improve decision making around farming.
The ITC Faculty of the University of Twente in the Netherlands has led a consortium of some of the world’s leading minds on agricultural remote sensing over a project period of 26 months (2014-1016). The consortium tested a number of hypotheses about the feasibility of agro- information products and assessed which types of information are most beneficial to stakeholders.
The consortium included an international group of research institutes:
- CSIRO/Australia,
- ICRISAT/Mali operating in Mali and Nigeria,
- University of Maryland/USA, operating in Tanzania and Uganda, and
- CIMMYT/Bangladesh operating in Bangladesh and Mexico.
The last three teams conducted regional use case experiments.
In West Africa (Nigeria and Mali), STARS activities aimed at providing a sustainable, subscription-based rural land tenure information service, supported by very high-resolution satellite imagery. It became clear that due to low volume of rural land transactions, only bundling such a service with other agronomic advisory services could be viable. STARS results were sufficiently compelling to trigger the emergence of a public-private partnership (PPP) joint-venture on digital agriculture, with EO industry (data), academia and NGO’s (knowledge) and input suppliers, insurers, agro-processors etc. (services).

In East Africa tools have been developed to support Nation-Wide Agriculture Monitoring for Food Security in Tanzania and Uganda. One of the main tools is a monthly national food security bulletin enabling the Ministry to make informed decisions.

The goal of our team in South Asia was a sustainable intensification of crop production in the southern delta of Bangladesh, through a field-specific irrigation advisory system in conjunction with integrated services. This has led to the development of a prototype of a field specific irrigation scheduling smartphone app (Program for Advanced Numerical Irrigation or PANI) that takes into account salinity and potential contribution of the water table to crop growth. The app informs farmers and irrigation service providers on a weekly basis whether a field needs to be irrigated. Like in the West African use case, PPP along with bundling of services (credit, telecom, solar energy supplier for irrigation, etc.) will be the key strategy to promote PANI as a sustainable social business solution.
Besides these regional activities, STARS produced a number of information products. These global public goods are:
- a Landscaping Report. The STARS Landscaping Study developed guidance on how remote sensing can help to build more effective systems for supporting agricultural development and poverty alleviation. The study reviewed the systems context, reviewed recent advances in remote sensing and geo-spatial technologies, and identified ten broad opportunities for remote sensing.
- a collection of image workflow and analysis algorithms that allow working with remote sensing images for smallholder monitoring and support, and
- a collection of crop spectral profiles, attributed with rich field data that aims to support follow-up studies of crop (type/growth)
The project website is offline as of September 2022, 5 years after the project was closed. For further details about the project, please contact us at: stars-itc@utwente.nl

